今回の計算tipsでは、
面積図・分配法則を利用する計算
をご紹介します。
1問目は99×99-98×100です。
まずは面積図を利用した解き方をご紹介します。
99×99は「たて99・横99の正方形の面積」
98×100は「たて98・横100の長方形の面積」
と考えることができますね。
2つの四角形を重ねると、このようになります。
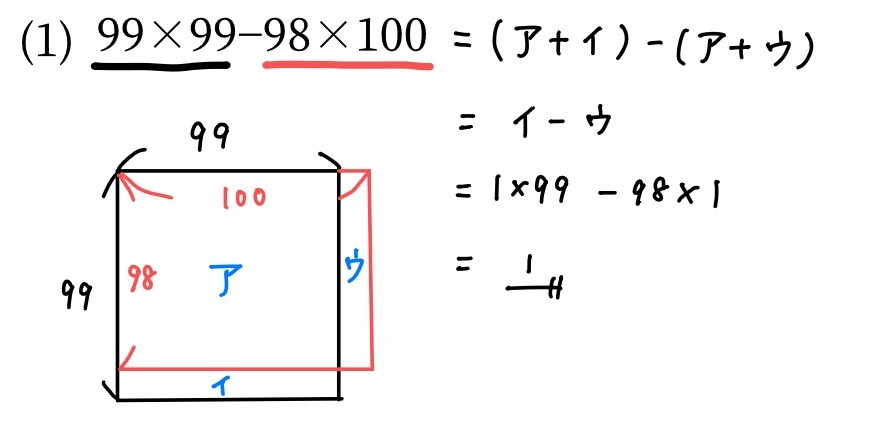
図の3か所の面積をそれぞれア・イ・ウとおくと
99×99は「たて99・横99の正方形の面積」なのでア+イ
98×100は「たて98・横100の長方形の面積」 なのでア+ウ
つまり
99×99- 98×100
=(ア+イ)-(ア+ウ)
=イ-ウ
=99-98
=1
と求められます。
次は分配法則を利用した解き方です。
‐98×100「98を100個引く」
−98×99 −98×1「98を99個引いた後に、98を1個引く」
は同じことを表しているので、
それを利用して計算していきます。
それを利用して計算していきます。
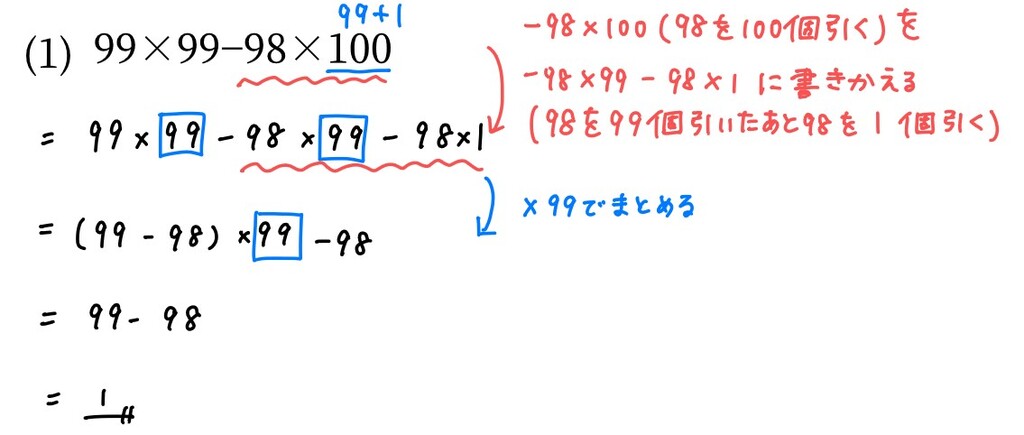
どちらの方法でも筆算はせず、暗算で解き進めることができます!
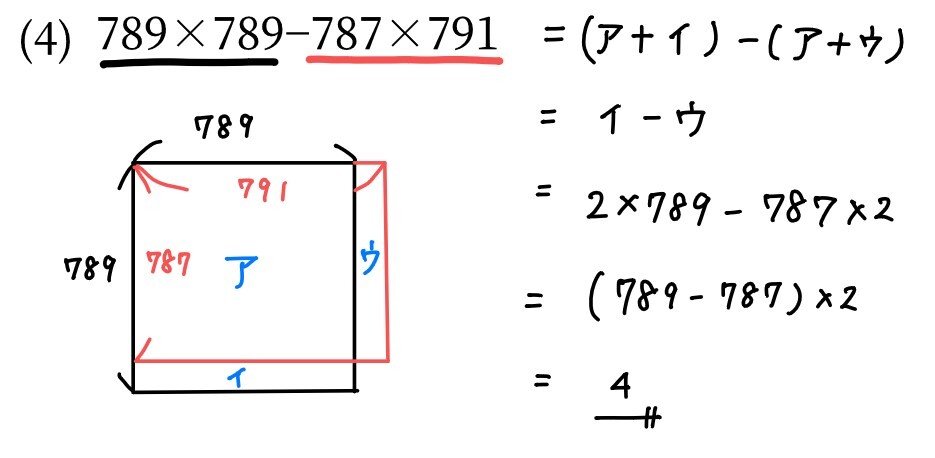
2問目は789×789-787×791です。
桁数も増えて難しそうですが、同じ解き方で答えを出せます。
桁数も増えて難しそうですが、同じ解き方で答えを出せます。

最後は999×999×999-998×999×1000です。
3つの数のかけ算ですが、共通している×999でまとめると
面積図・分配法則に持ち込むことができます!

999×999×999-998×999×1000
大変そうに見える計算でしたが、面積図や分配法則を使うと簡単に答えを導くことができましたね。
ちなみに面積図・分配法則はどちらを使ってもOKです!
好みの解き方でやってみてください。
3つの数のかけ算ですが、共通している×999でまとめると
面積図・分配法則に持ち込むことができます!

大変そうに見える計算でしたが、面積図や分配法則を使うと簡単に答えを導くことができましたね。
ちなみに面積図・分配法則はどちらを使ってもOKです!
好みの解き方でやってみてください。
